Zum Ausdrucken die Abschnitte aufklappen, die gedruckt werden sollen.
Lagemaße
Arithmetisches Mittel
Das Arithmetische Mittel (oder einfach nur der Mittelwert) ist der Durchschnitt einer Datenreihe.
Glossar S.22
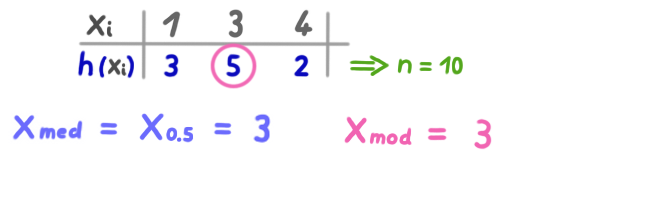
Median
Der Median ist die Mitte der geordneten Datenreihe.
Glossar S.21
Modalwert
Der Modalwert (oder Modus) ist der Wert, der am häufigsten vorkommt.
Glossar S.23
Lagemaße mit Häufigkeitstabelle
Beispiel mit absoluten Häufigkeiten:
Beispiel mit relativen Häufigkeiten:
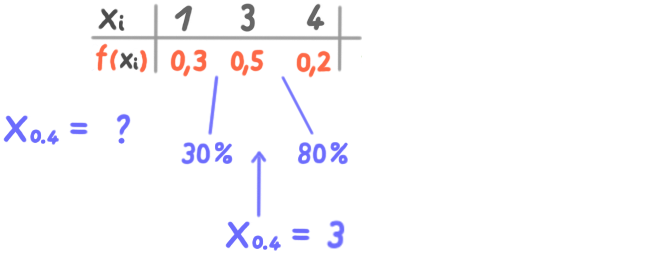
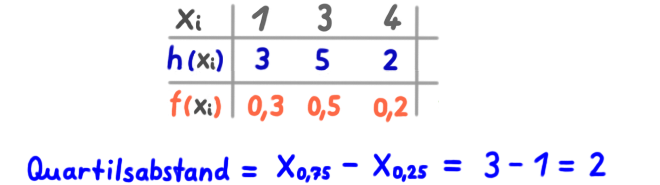
Quantile
Das p-Quantil xp ist derjenige Wert der geordneten Datenreihe, bis zu dem sich p Prozent aller Werte befinden.
Einfaches Beispiel:
Zur Ermittlung eines beliebigen Quantils einer beliebigen Datenreihe, wie folgt vorgehen:
Glossar S.25
Beispiel:
Beispiel mit Häufigkeitstabelle:
Beispiel mit relativen Häufigkeiten:
Varianz
Die Varianz ist die durchschnittliche quadratische Abweichung.
Einfaches Beispiel:
Alternative Formel:
Standardabweichung
Die Standardabweichung ist die Wurzel der Varianz.
Beispiel:
Häufigkeitstabellen
Beispiel mit absoluten Häufigkeiten:
Beispiel mit relativen Häufigkeiten:
Kovarianz
Die Kovarianz ist eine Maßzahl dafür, wie 2 Merkmale gemeinsam variieren.
Beispiel:
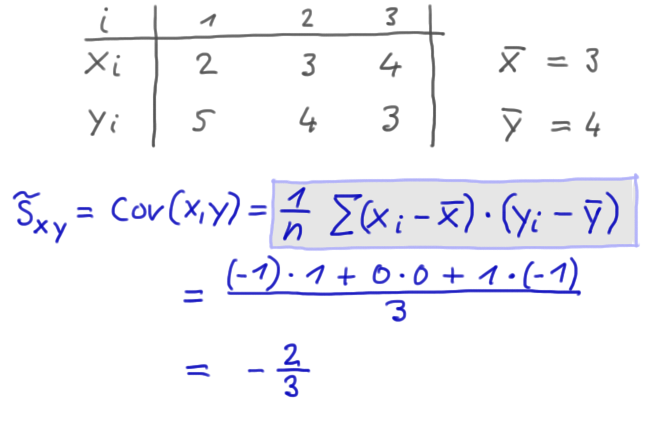
Glossar S.18
Beispiel mit Häufigkeitstabelle:

Glossar S.18
Bravais-Pearson
Der Korrelationskoeffizient nach Bravais-Pearson ist die normierte Kovarianz.
Die Kovarianz wird ins Verhältnis gesetzt zur maximal möglichen Kovarianz. Die maximal mögliche Kovarianz ist das Produkt der Standardabweichungen (oder die Wurzel des Produktes der Varianzen).
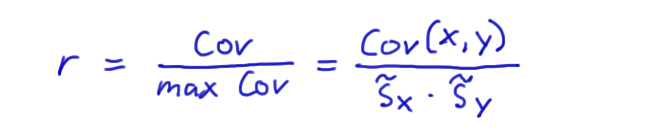
Glossar S.17
Beispiel:

Spearman
Der Korrelationskoeffizient nach Spearman ist die Korrelation der Rangzahlen, welche wiederum die normierte Kovarianz der Rangzahlen ist.

Glossar S.18
Im ersten Schritt werden den Werten der Einzelmerkmale Rangzahlen zugeordnet. Im zweiten Schritt wird für diese Rangzahlen dann eine Korrelation ausgerechnet.
Beispiel:

Verkürzter Rechenweg:
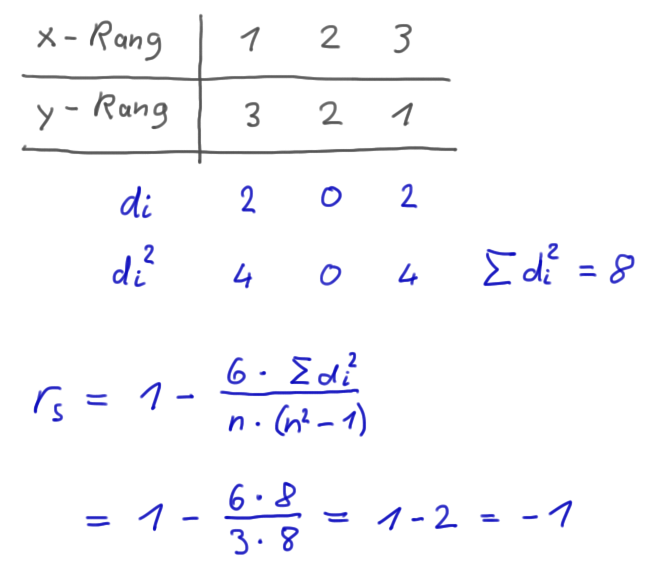
Glossar S.18
Um diese Inhalte zu nutzen, musst du dich anmelden.
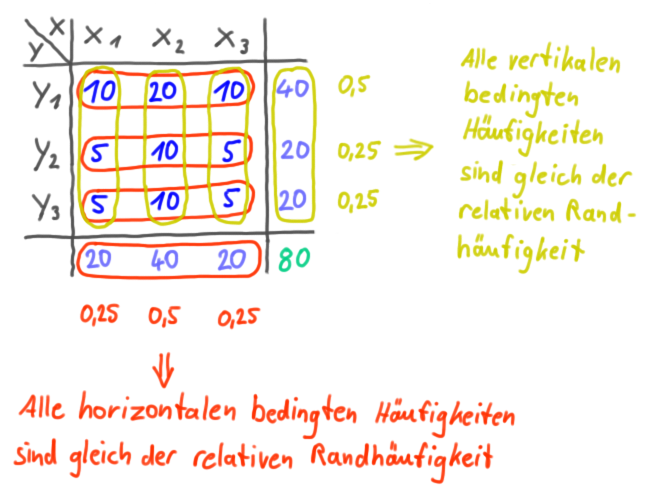
Empirische (Un-) Abhängigkeit
Zwei Merkmale sind empirisch unabhängig voneinander, wenn in einer zweidimensionalen Häufigkeitstabelle alle bedingten Häufigkeiten gleich der relativen Randhäufigkeit sind.
Beispiel für empirische Unabhängigkeit:
=> Die Merkmale X und Y sind unabhängig
Wenn auch nur eine einzige Häufigkeit ein klein wenig von der Verteilung bei völliger Unabhängigkeit abweicht, nennt man die Merkmale empirisch abhängig.
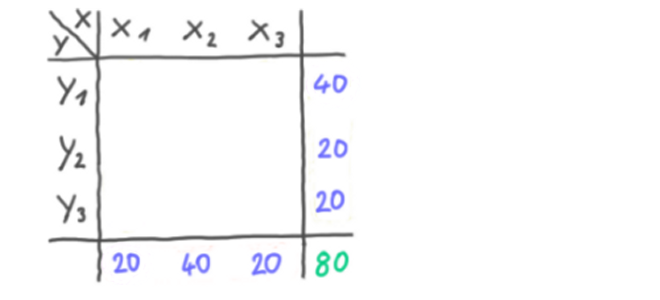
Beispiel für empirische Abhängigkeit:
Kontingenzkoeffizient
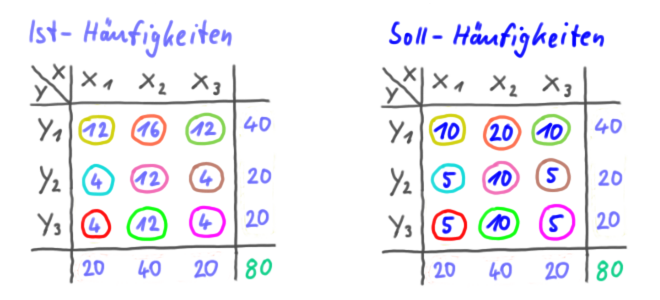
Der Kontingenzkoeffizient ist der „Korrelationskoeffizient für nominale Merkmale“. Um den Kontingenzkoeffizient zu ermitteln, muss man zunächst Chi-Quadrat (X2) ausrechnen.
Chi-Quadrat (X2) ist eine Maßzahl für die Abweichung von der völligen Unabhängigkeit. Um also Chi-Quadrat auszurechnen, muss man erstmal wissen, wie die Soll-Häufigkeiten bei völliger Unabhängigkeit sind.
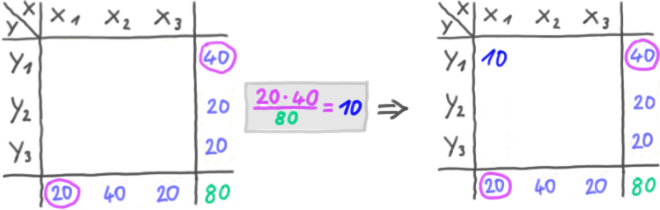
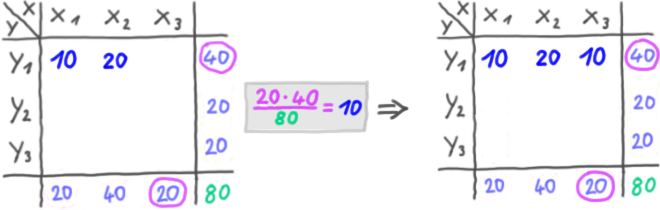
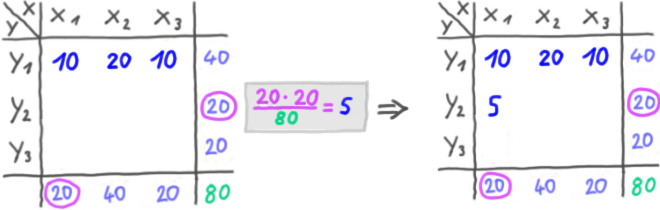
Wie also sind die Soll-Häufigkeiten? Die Soll-Häufigkeiten werden mithilfe der Randhäufigkeiten ausgerechnet.
Beispiel:
Wir multiplizieren die jeweiligen Randhäufigkeiten und teilen durch die Gesamthäufigkeit:
usw.
Jetzt haben wir die Soll-Häufigkeiten und können Chi-Quadrat (X2) ausrechenen.
Beispiel:
Glossar S.17
Der Kontingenzkoeffizent C kann jetzt anhand von X2 und der Gesamthäufigkeit n = 80 ausgerechnet werden:
Glossar S.17
Jetzt kann auch noch der korrigierte Kontingenzkoeffizent Ckorr ausgerechnet werden:
Glossar S.17
C* ist dabei der kleinere Wert aus Zeilen- und Spaltenanzahl. Wir haben 3 Zeilen und 3 Spalten, also ist C*= 3.
Skalenniveaus
Grundsätzlich unterscheidet man zwischen drei verschiedenen Skalenniveaus:
- metrisch
- ordinal
- nominal
Metrische Merkmale haben solche Werte mit denen man rechnen kann. Man kann sie addieren, subtrahieren oder den Durchschnitt berechnen. Es gibt definierte Abstände. Der Abstand zwischen 1 und 3 ist immer genauso groß, wie der Abstand zwischen 3 und 5.
Beispiele für metrische Größen:
- Länge (30 cm)
- Gewicht (50 kg)
- Anzahl (8 Äpfel)
Ordinale Merkmale haben Werte mit denen man nicht rechnen kann. Ordinale Merkmale erkennt man daran, dass ihre Werte entweder Buchstaben sind, oder durch Buchstaben ersetzt werden könnten, ohne dabei irgendwelche Informationen zu verlieren. Es gibt eine Rangfolge, aber es gibt keine Abstände zwischen zwei Werten. Man weiß nur, dass ein Wert mehr oder weniger ist als ein anderer Wert, aber nicht WIEVIEL mehr oder weniger. Man kann keinen Durchschnitt berechnen. Es gibt also kein arithmetisches Mittel, nur Median und Modalwert.
Beispiele für ordinale Größen:
- Bonitätsnote (AAA > AA > A > B)
- Dienstrang beim Militär (General > Leutnant > Unteroffizier > Gefreiter)
- Zufriedenheit mit einem Produkt (sehr zufrieden > eher zufrieden > eher unzufrieden > sehr unzufrieden)
Nominale Merkmale kennen kein mehr oder weniger, nur gleich oder ungleich. Es gibt also kein arithmetisches Mittel und auch keinen Median. Es gibt nur den Modalwert.
Beispiele für nominale Größen:
- Nationalität (schwedisch ≠ italienisch ≠ deutsch)
- Haarfarbe (blond ≠ schwarz ≠ braun)
- Studienfach (Wiwi ≠ Psychologie ≠ Physik)
Unterschiedliche metrische Skalenniveaus
Bei metrischen Merkmalen unterscheidet man noch zwischen:
- Intervall-Skala
- Verhältnis-Skala
- Absolut-Skala
Die meisten metrischen Merkmale sind auf einer Verhältnis-Skala. Sie haben einen natürlichen Nullpunkt.
– 0 Meter
– 0 kg
– 0 Euro
Verschiedene Werte kann man immer ins Verhältnis zueinander setzen. 10 Meter ist doppelt so viel wie 5 Meter: 10m/5m = 2.
Intervall-skalierte Merkmale kann man nicht ins Verhältnis zueinander setzen. Ein Beispiel ist die Temperatur in Grad Celsius. Hier gibt es KEINEN natürlichen Nullpunkt. Der Nullpunkt wurde „willkürlich“ festgelegt, beim Gefrierpunkt. Aber zwei verschiedene Werte haben immer einen definierten Abstand – ein Intervall. Metrische Merkmale sind immer mindestens intervall-skaliert.
Auf einer anderen Skala – der Temperatur in Kelvin – HAT die Temperatur einen natürlichen Nullpunkt und ist somit verhältnis-skaliert.
Die Absolut-Skala bezeichnet Stückzahlen, wie etwa die Anzahl Äpfel. Sie braucht keine „künstliche“ Größeneinheit wie Meter oder kg.



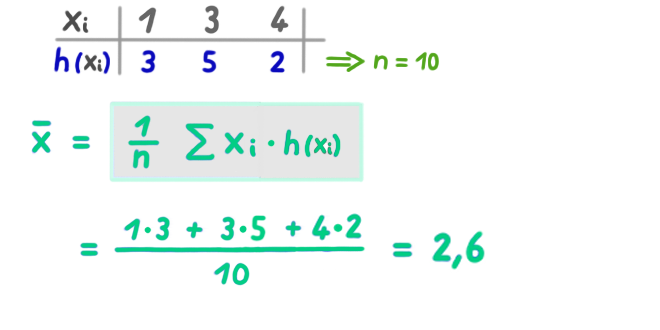


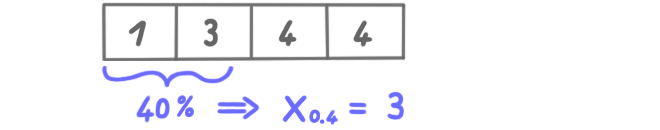


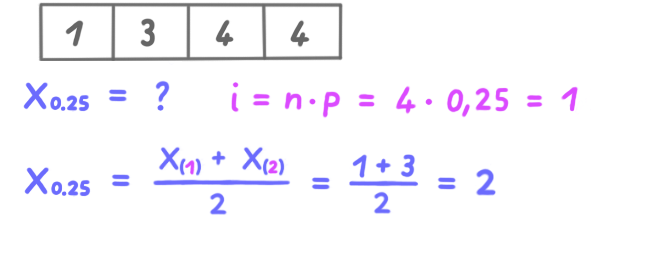
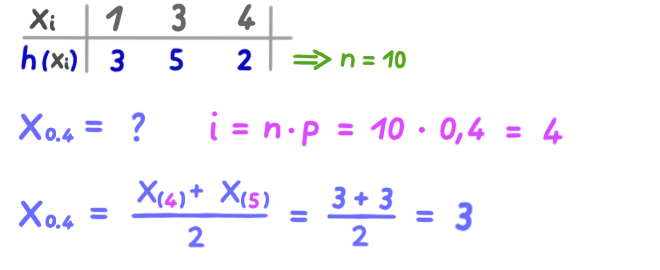
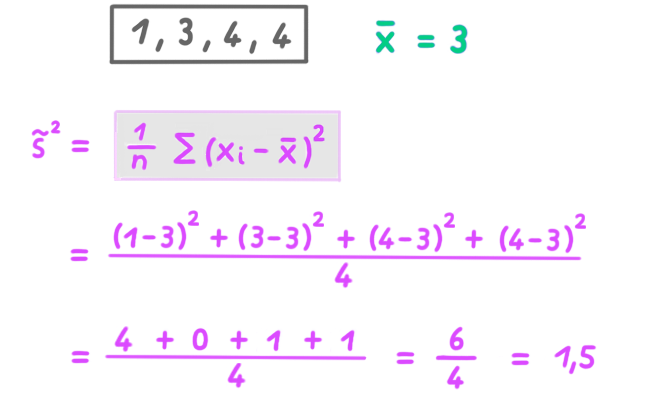

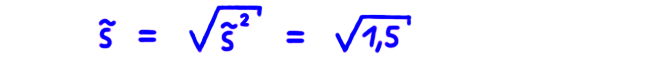
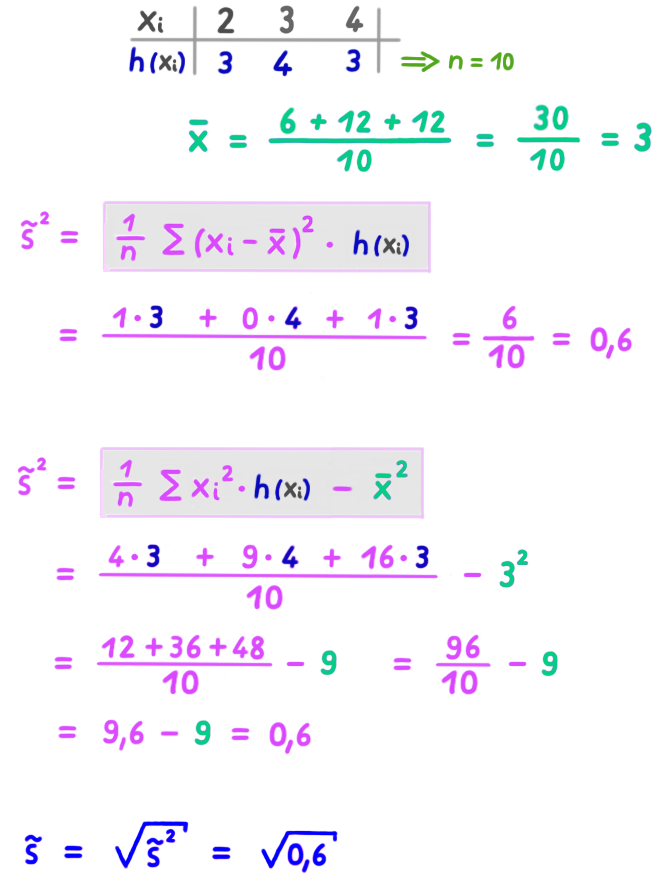





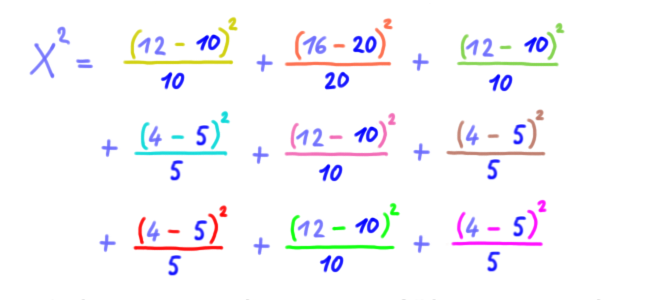



Okay. Ich bin hier Quereinsteigerin (Psychologie B.Sc.).
Hallo Guido,
lieben Dank für diese wunderbare hilfreiche Seite.
Wo finde ich denn eigentlich das Glossar?
Herzliche Grüße
Sigrid
Hallo Sigrid, das Glossar ist eines der Skripte des Kurses 40601 im Studiengang Bachelor Wirtschaftswissenschaften in Hagen 🙂