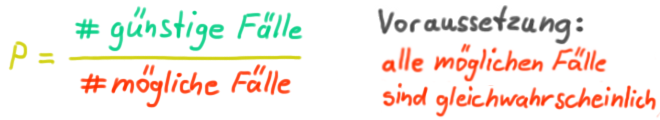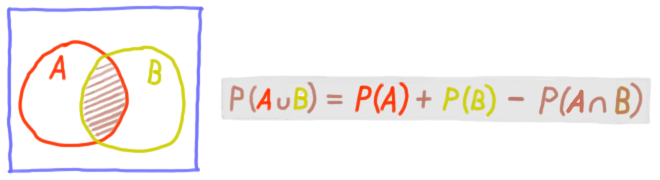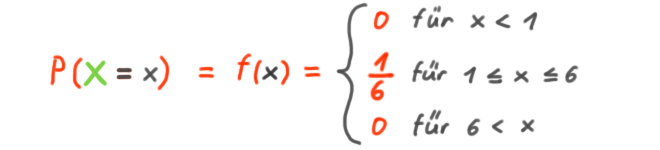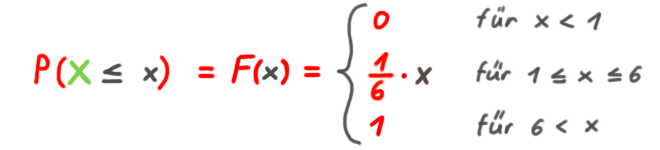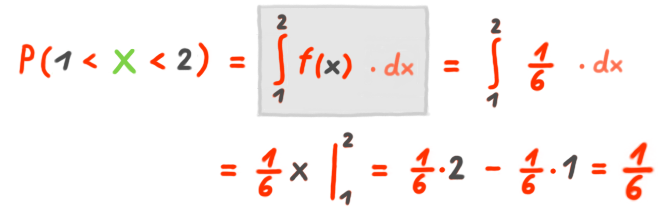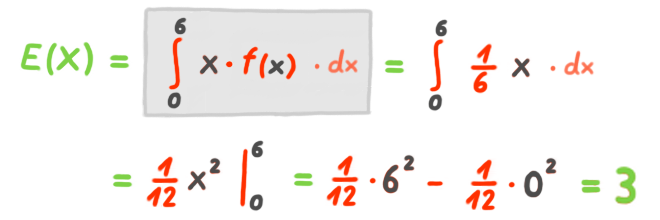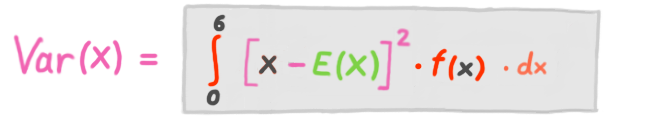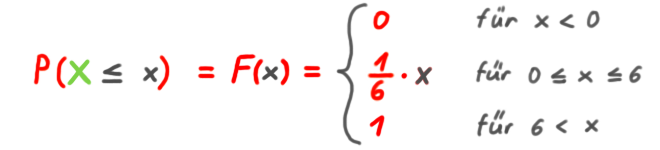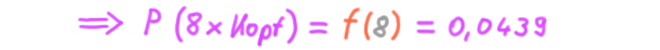Wahrscheinlichkeits-Rechnung

Zum Ausdrucken die Abschnitte aufklappen, die gedruckt werden sollen.

Seite drucken

Grundlagen

Ermittlung von Wahrscheinlichkeiten

In der WSK-Rechnung geht es primär darum, wie man mit WSKen rechnet. Aber wie ermittelt man die Ausgangs-WSKen?

Zwei Möglichkeiten:

1. WSK nach Laplace

Glossar S.38

Beispiel: Das Werfen eines Würfels. Die WSK für eine gerade Zahl ist 3 aus 6.

2. WSK nach der statistischen Definition

Glossar S.38

Die WSKen entsprechen den relativen Häufigkeiten (wie auch in diesem Video erläutert).

Je größer n, desto mehr entsprechen die relativen Häufigkeiten den WSKen (Gesetz der großen Zahlen).

WSK-Rechnung im engeren Sinn

Bei der WSK-Rechnung im engeren Sinn geht es darum, wie man mit WSKen rechnet.

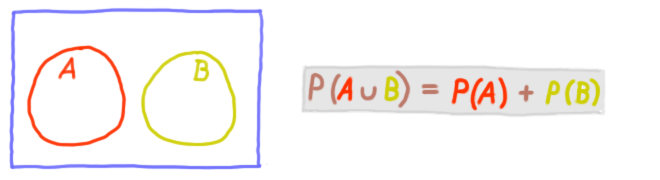
☝️ Die Summe aller Wahrscheinlichkeiten ist immer 1.

Additionssatz für zwei sich ausschließende Ereignisse:

(ein Ereignis ist das Ergebnis eines Zufallsexperiments)

Glossar S.8

Additionssatz für zwei beliebige Ereignisse:

Glossar S.8

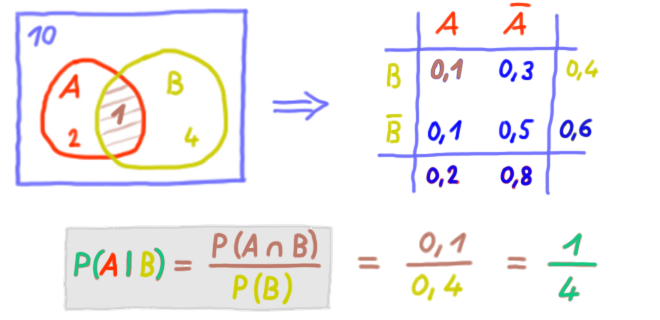
Bedingte WSK:

(gesprochen „P von A nach B“)

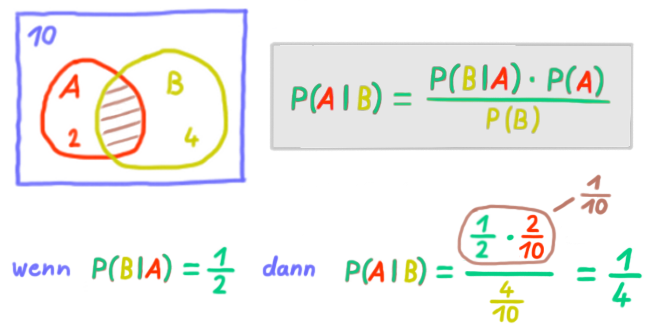
☝️ Die bedingte WSK ist der prozentuale Anteil, den die Zelle an ganz B hat.

Daraus ergibt sich der Multiplikationssatz für beliebige Ereignisse:

Glossar S.9

Das ist die bedingte WSK umgedreht.

In Worten: Ein Viertel von 0,4 ist 0,1.

Allgemeiner: Die bedingte WSK mal die WSK für die Bedingung ergibt die WSK für die Zelle.

Stochastische (Un-)Abhängigkeit

Das Prinzip der stochastischen Unabhängigkeit ist identisch zur empirischen Unabhängigkeit. Aber hier mit WSKen statt Häufigkeiten.

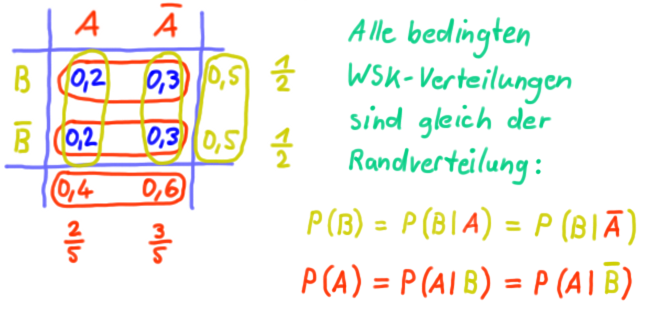
Zwei Ereignisse sind stochastisch unabhängig voneinander, wenn alle bedingten WSKen gleich der Randverteilung sind.

Glossar S.9

Daraus ergibt sich der Multiplikationssatz für unabhängige Ereignisse:

Glossar S.9

☝️ Die Begriffe Additionssatz, Multiplikationssatz, etc. wurden bisher nie abgefragt. Wichtig sind vor allem die Zusammenhänge, wie auch mit den Lernkarten eingeübt.

Satz von Bayes

+ Zufallsvariablen
- Zufallsvariablen allgemein

Zufallsvariablen

Zufallsvariablen nehmen das Ergebnis eines Zufallsexperiments auf.

Beispiel:

Die Zufallsvariable X nimmt das Ergebnis eines Würfelwurfs auf.

WSK-Verteilung

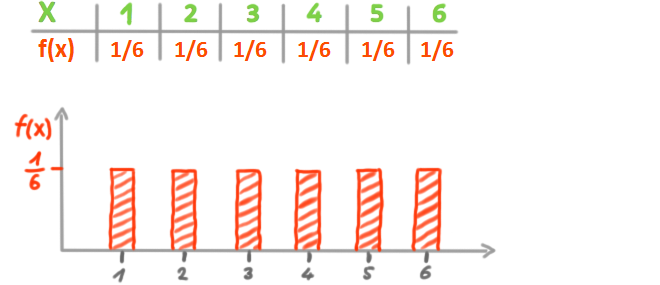
Somit hat die Zufallsvariable X diese WSK-Verteilung:

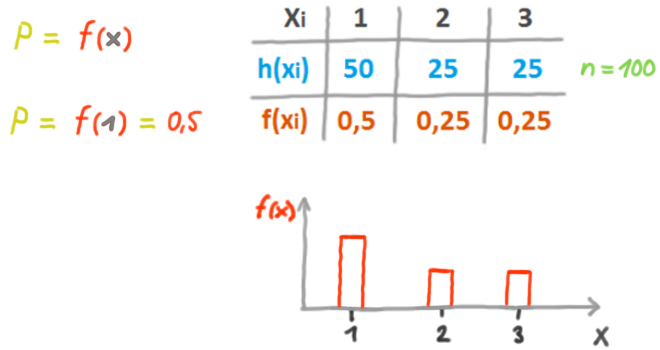
WSK-Funktion

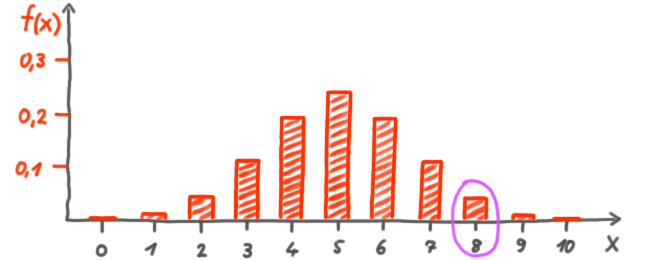
f(x) ist die WSK-Funktion der Zufallsvariablen:

Die WSK, dass die Zufallsvariable Groß X einen der durch klein x repräsentierten Werte annimmt, ist 1/6 für jeden Wert von 1 bis 6.

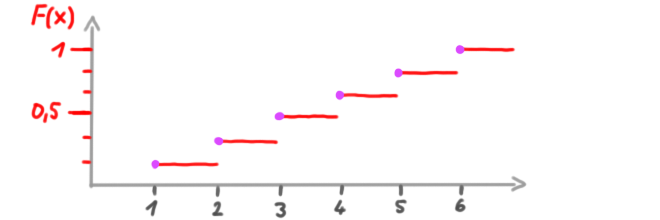
Verteilungs-Funktion

F(x) ist die Verteilungs-Funktion (äquivalent zur Summenhäufigkeit in der deskriptiven Statistik).

Zusammengefasst

Zufallsvariablen unterscheiden sich von „normalen“ Variablen dadurch, dass sie – BEVOR sie einen konkreten Wert haben, also BEVOR das Zufallsexperiment durchgeführt wurde – eine WSK-Verteilung /-Funktion haben.

☝️Zufallsvariablen haben eine WSK-Verteilung.

- Diskrete Zufallsvariablen 🔒/🔓€

Diskrete Zufallsvariablen

Vorbemerkung: In der deskriptiven Statistik hatten wir Merkmale und deren Häufigkeitsverteilungen. In der WSK-Rechnung haben wir Zufallsvariablen und deren WSK-Verteilungen.
☝️Zufallsvariablen haben genau die gleichen Lagemaße, Streuungsmaße und Zusammenhangsmaße wie die Merkmale aus der deskriptiven Statistik.
Um diese Inhalte zu nutzen, musst du dich anmelden und den vollen Zugriff für den Kurs kostenpflichtig erwerben.

- Stetige Zufallsvariablen

Stetige Zufallsvariablen

☝️Allgemeine Rechenaufgaben zu stetigen Zufallsvariablen und WSK-Verteilungen kamen in den letzten Jahren nicht in der Klausur dran (siehe Aufgaben-Statistiken und die einzige Ausnahme). Stattdessen kamen Aufgaben für die Normalverteilung, einer besonderen Form der stetigen WSK-Verteilung. Bei der Normalverteilung werden die WSKen aber nicht über das Integral der Dichtefunktion berechnet (wie folgend dargestellt), sondern aus WSK-Tabellen abgelesen. Der Erwartungswert und die Varianz sind bei solchen Aufgaben idR gegeben. Somit sind die Inhalte dieser Zusammenfassung voraussichtlich nicht klausurrelevant.

Eine stetige ZV hat eine stetige WSK-Verteilung.

Beispiel Gleichverteilung für alle Werte zwischen 0 und 6:

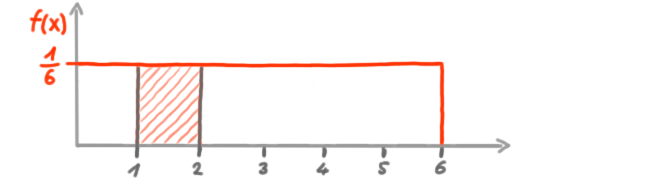
Und eine Dichtefunktion:

Die Dichtefunktion einer stetigen ZV liefert nicht die WSK für einen bestimmten Wert – so wie die WSK-Funktion einer diskreten ZV – sondern nur die WSK-Dichte. Die WSK muss über das Integral der Dichtefunktion (die Fläche unter der Kurve) ausgerechnet werden.

Die WSK für einen Wert zwischen 1 und 2 ist die Fläche unter der Kurve zwischen 1 und 2:

Erwartungswert

Den Erwartungswert einer stetigen ZV / Dichtefunktion berechnet man wie folgt:

Glossar S.10

Varianz

Die Varianz einer stetigen ZV / Dichtefunktion berechnet man wie folgt:

Glossar S.35

Glossar S.35

Verteilungsfunktion

Die Verteilungsfunktion ist nicht stufig – so wie bei einer diskreten ZV – sondern sieht für die obige Dichtefunktione wie folgt aus :

Binomialverteilung

Binomialverteilung

Bei der Binomialverteilung geht es immer um eine Serie von binären Ereignissen, wie z.B. das mehrfache Werfen einer Münze. Wenn wir eine Münze zehnmal werfen, wie wahrscheinlich ist es, dass sie acht mal mit der Kopfseite oben landet.

In Tabellenform sieht das so aus:

Normalverteilung

Normalverteilungs-Kurve

Eine Normalverteilungs-Kurve ist vollständig beschrieben durch die beiden Parameter μ und σ – (Mü und Sigma).

Den Z-Wert eines beliebigen x-Wertes rechnet man:

☝️Der Z-Wert ist die Abweichung bezogen auf die Standardabweichung. Wie viele Standardabweichungen ist der x-Wert vom Mittelwert entfernt?

Anhand des Z-Wertes kann man die verschiedenen WSKen dann aus einer WSK-Tabelle ablesen.

WSK-Tabelle einer Normalverteilung

Kombination von Zufallsvariablen 🔒/🔓€
Um diese Inhalte zu nutzen, musst du dich anmelden und den vollen Zugriff für den Kurs kostenpflichtig erwerben.

Schreibe einen Kommentar