Zum Ausdrucken die Abschnitte aufklappen, die gedruckt werden sollen.
Inferenzstatistik
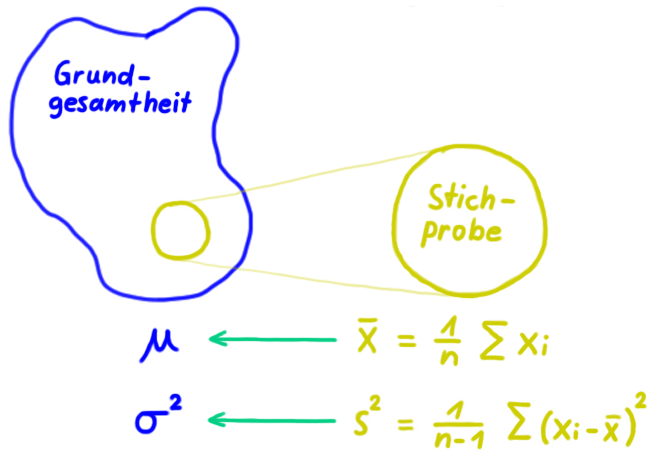
In der Inferenzstatistik geht es darum, die Parameter einer Grundgesamtheit mithilfe einer Stichprobe zu schätzen.
Je größer die Stichprobe, desto genauer die Schätzung.
Bei einem Stichproben-Umfang größer 30 kann man anhand des Zentralen Grenzwertsatzes die WSKen für die Genauigkeit der Schätzung bestimmen.
Zentraler Grenzwertsatz
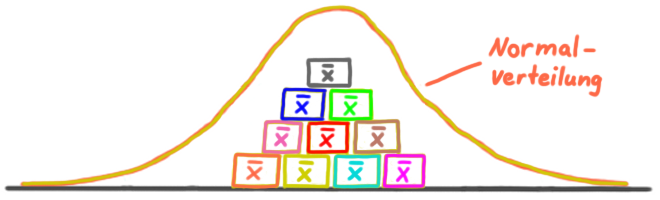
Der Zentrale Grenzwertsatz besagt, dass die Verteilung der Stichproben-Mittelwerte – für Stichproben > 30 – eine Normalverteilung ist.
Jedes X quer ist der Mittelwert einer Stichprobe.
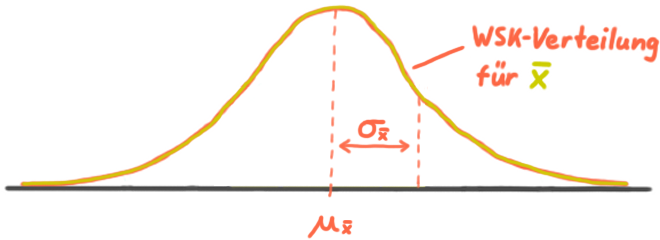
Diese Häufigkeits-Verteilung der Stichproben-Mittelwerte ist gleichzeitig auch eine WSK-Verteilung für jeden einzelnen Stichproben-Mittelwert.
Für irgendeinen Stichproben-Mittelwert gilt also:
Die WSK, dass ein Stichproben-Mittelwert innerhalb einer Standardabweichung vom Mittelwert der Stichproben-Mittelwerte liegt, ist 68 Prozent.
Dabei gilt:
μ und σ sind die Parameter der Grundgesamtheit, aus der die Stichprobe entnommen wurde.
Daher nennt man den Stichproben-Mittelwert ![]() als Schätzwert für μ erwartungstreu.
als Schätzwert für μ erwartungstreu.
Konfidenzintervalle
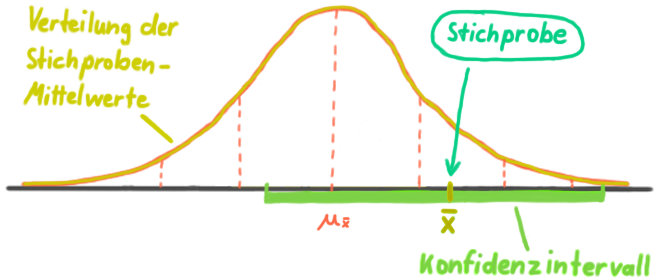
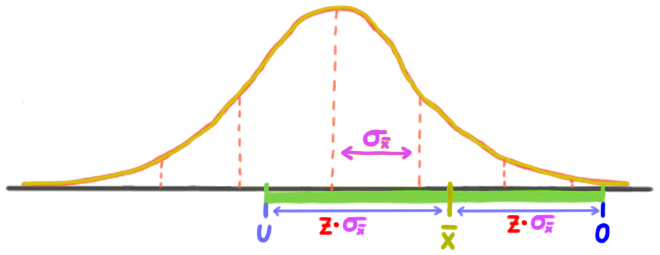
Ein Konfidenzintervall für den Mittelwert μ der Grundgesamtheit ist ein Schätzintervall, das um den Mittelwert ![]() einer Stichprobe gebildet wird.
einer Stichprobe gebildet wird.
![]() ist ein Schätzwert für μ. Das Konfidenzintervall ist ein Schätzintervall für μ.
ist ein Schätzwert für μ. Das Konfidenzintervall ist ein Schätzintervall für μ.
Um das Konfidenzintervall für ein bestimmtes Konfidenzniveau zu bestimmen, benötigen wir den Z-Wert für dieses Konfidenzniveau.
Diesmal suchen wir also nicht die WSK für einen Z-Wert, sondern den Z-Wert für eine WSK. Auch dazu schauen wir in die Tabelle:
Der Z-Wert für ein ZWEISEITIGES Konfidenzintervall zum Konfidenzniveau von 95 Prozent ist 1,96.
Für das zweiseitige Konfidenzintervall brauchen wir also den Bereich innerhalb von 1,96 Standardabweichungen um ![]() .
.
Einseitige Konfidenzintervalle
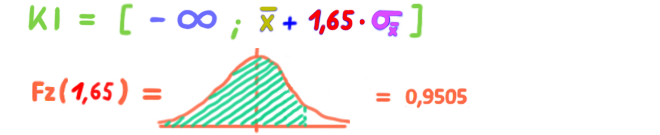
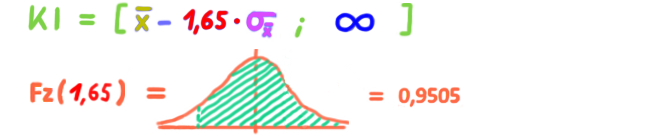
Der Z-Wert für ein EINSEITIGES Konfidenzintervall zum Konfidenzniveau von 95 Prozent ist 1,65.
1,64 ginge auch
Je nachdem ob die rechte oder linke Seite gesucht ist:
oder:
Berechnung mit Z-Quantilen
Um diese Inhalte zu nutzen, musst du dich anmelden und den vollen Zugriff für den Kurs kostenpflichtig erwerben.
Um diese Inhalte zu nutzen, musst du dich anmelden und den vollen Zugriff für den Kurs kostenpflichtig erwerben.
Um diese Inhalte zu nutzen, musst du dich anmelden und den vollen Zugriff für den Kurs kostenpflichtig erwerben.
Um diese Inhalte zu nutzen, musst du dich anmelden und den vollen Zugriff für den Kurs kostenpflichtig erwerben.
Um diese Inhalte zu nutzen, musst du dich anmelden und den vollen Zugriff für den Kurs kostenpflichtig erwerben.
Um diese Inhalte zu nutzen, musst du dich anmelden und den vollen Zugriff für den Kurs kostenpflichtig erwerben.