Überblick Woche 13+14
Zentraler Grenzwertsatz
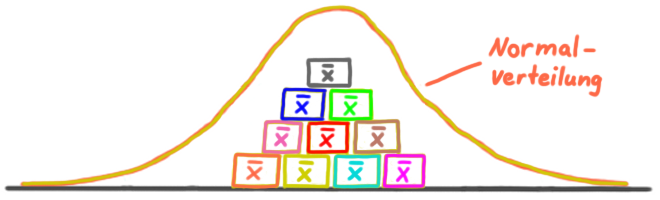
Der Zentrale Grenzwertsatz besagt, dass die Verteilung der Stichproben-Mittelwerte – für Stichproben > 30 – eine Normalverteilung ist.
Jedes X quer ist der Mittelwert einer Stichprobe.
Diese Häufigkeits-Verteilung der Stichproben-Mittelwerte ist gleichzeitig auch eine WSK-Verteilung für jeden einzelnen Stichproben-Mittelwert.
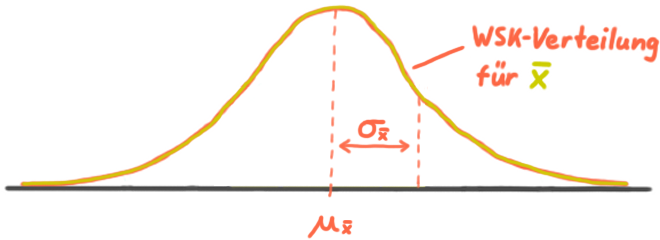
☝️Das ist die WSK-Verteilung der Stichproben-Mittelwerte.
Für irgendeinen Stichproben-Mittelwert gilt also:
Die WSK, dass ein Stichproben-Mittelwert innerhalb einer Standardabweichung vom Mittelwert der Stichproben-Mittelwerte liegt, ist 68 Prozent.
☝️Auch die WSK-Verteilung der Stichproben-Mittelwerte hat einen Mittelwert.
Dabei gilt:
μ und σ sind die Parameter der Grundgesamtheit, aus der die Stichprobe entnommen wurde.
☝️Der Durchschnitt der Stichproben-Mittelwerte (
) ist gleich dem Mittelwert μ der Grundgesamtheit.
) ist gleich dem Mittelwert μ der Grundgesamtheit.
Daher nennt man den Stichproben-Mittelwert 
als Schätzwert für μ erwartungstreu.
Randbemerkung: Somit könnte man eigentlich auch sagen, mit welcher WSK μ in der Nähe von 
ist. Es ist aber unüblich, WSK-Aussagen für μ zu machen, weil μ keine Zufallsvariable ist, sondern ein unbekannter, aber fester Parameter der Grundgesamtheit. Daher verwendet man andere Begriffe: man berechnet ein „Konfidenzintervall“ für ein bestimmtes „Konfidenzniveau“.
ist. Es ist aber unüblich, WSK-Aussagen für μ zu machen, weil μ keine Zufallsvariable ist, sondern ein unbekannter, aber fester Parameter der Grundgesamtheit. Daher verwendet man andere Begriffe: man berechnet ein „Konfidenzintervall“ für ein bestimmtes „Konfidenzniveau“.
☝️In der Klausur wird niemals eine solche Aufgabe drankommen, sondern nur Aufgaben zu Konfidenzintervallen und Hypothesentests.