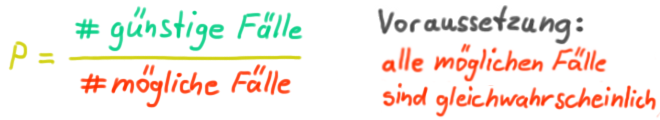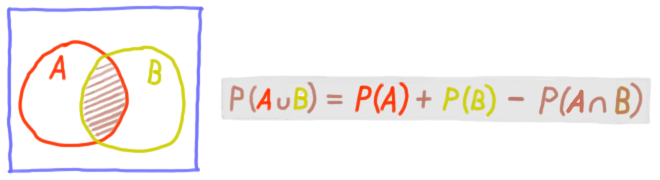Zusammenfassung Wahrscheinlichkeits-Rechnung

Überblick Woche 7+8

[Bitte erst die Lernkarten anschauen]

Ermittlung von Wahrscheinlichkeiten

In der WSK-Rechnung geht es primär darum, wie man mit WSKen rechnet. Aber wie ermittelt man die Ausgangs-WSKen?

Zwei Möglichkeiten:

1. WSK nach Laplace

_{Glossar S.38}

Beispiel: Das Werfen eines Würfels. Die WSK für eine gerade Zahl ist 3 aus 6.

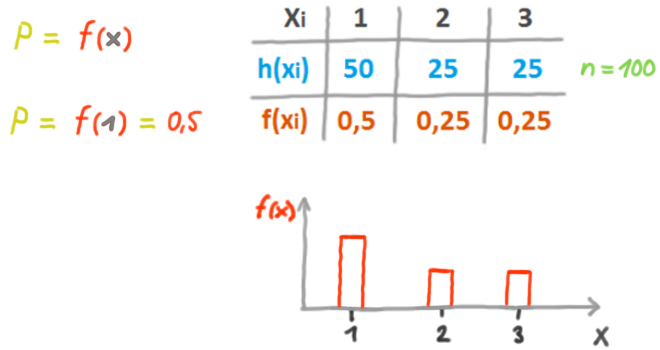
2. WSK nach der statistischen Definition

_{Glossar S.38}

Die WSKen entsprechen den relativen Häufigkeiten (wie auch in diesem Video erläutert).

Je größer n, desto mehr entsprechen die relativen Häufigkeiten den WSKen (Gesetz der großen Zahlen).

WSK-Rechnung im engeren Sinn

Bei der WSK-Rechnung im engeren Sinn geht es darum, wie man mit WSKen rechnet.

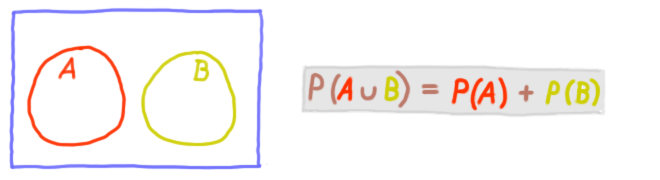
Additionssatz für zwei sich ausschließende Ereignisse:

^{(ein Ereignis ist das Ergebnis eines Zufallsexperiments)}

^{Glossar S.8}

Additionssatz für zwei beliebige Ereignisse:

^{Glossar S.8}

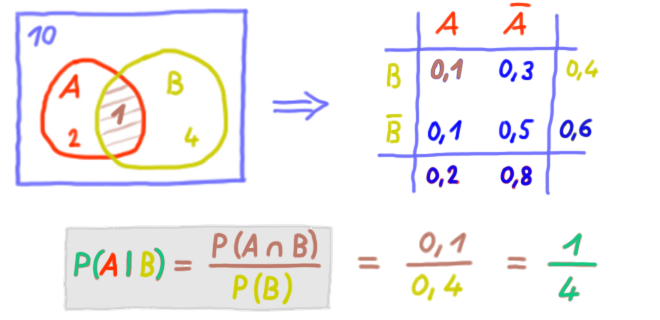
Bedingte WSK:

^{(gesprochen „P von A nach B“)}

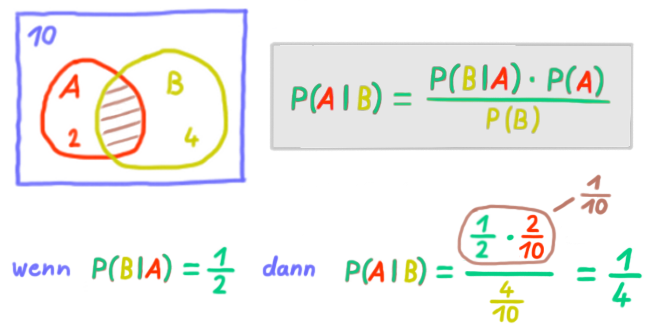
Daraus ergibt sich der Multiplikationssatz für beliebige Ereignisse:

^{Glossar S.9}

Das ist die bedingte WSK umgedreht.

In Worten: Ein Viertel von 0,4 ist 0,1.

Allgemeiner: Die bedingte WSK mal die WSK für die Bedingung ergibt die WSK für die Zelle.

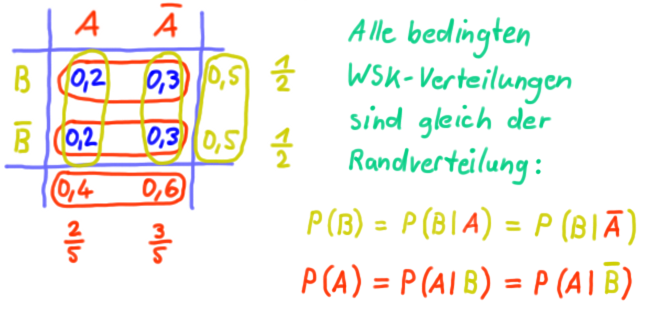
Stochastische (Un-)Abhängigkeit

Das Prinzip der stochastischen Unabhängigkeit ist identisch zur empirischen Unabhängigkeit. Aber hier mit WSKen statt Häufigkeiten.

Zwei Ereignisse sind stochastisch unabhängig voneinander, wenn alle bedingten WSKen gleich der Randverteilung sind.

^{Glossar S.9}

Daraus ergibt sich der Multiplikationssatz für unabhängige Ereignisse:

^{Glossar S.9}

Satz von Bayes