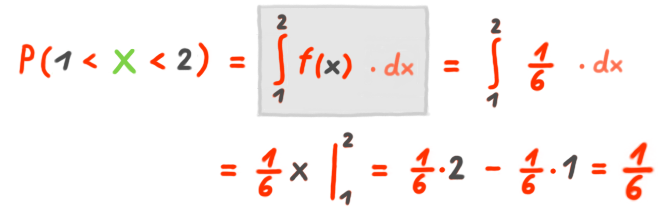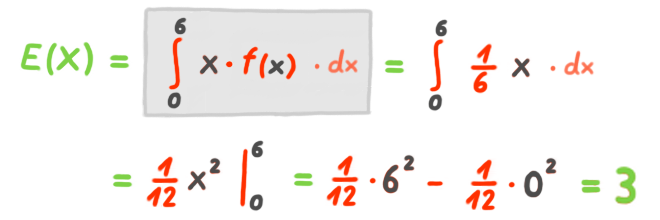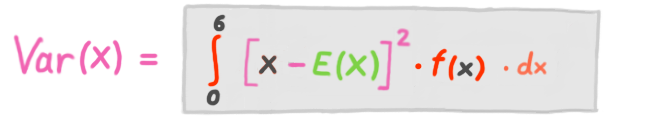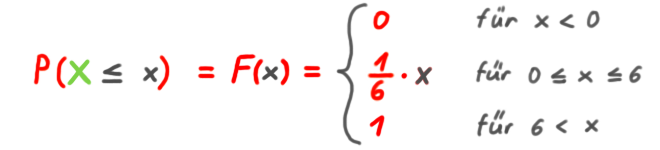Zusammenfassung stetige Zufallsvariablen

Überblick Woche 9+10

Stetige Zufallsvariablen

Eine stetige ZV hat eine stetige WSK-Verteilung.

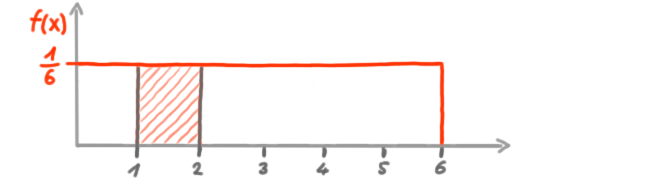
Beispiel Gleichverteilung für alle Werte zwischen 0 und 6:

Und eine Dichtefunktion:

Die Dichtefunktion einer stetigen ZV liefert nicht die WSK für einen bestimmten Wert – so wie die WSK-Funktion einer diskreten ZV – sondern nur die WSK-Dichte. Die WSK muss über das Integral der Dichtefunktion (die Fläche unter der Kurve) ausgerechnet werden.

Die WSK für einen Wert zwischen 1 und 2 ist die Fläche unter der Kurve zwischen 1 und 2:

Erwartungswert

Den Erwartungswert einer stetigen ZV / Dichtefunktion berechnet man wie folgt:

^{Glossar S.10}

Varianz

Die Varianz einer stetigen ZV / Dichtefunktion berechnet man wie folgt:

^{Glossar S.35}

^{Glossar S.35}

Verteilungsfunktion

Die Verteilungsfunktion ist nicht stufig – so wie bei einer diskreten ZV – sondern sieht für die obige Dichtefunktione wie folgt aus :